2023. 1. 4. 17:44ㆍJava/coding test
PassingCars
A non-empty array A consisting of N integers is given. The consecutive elements of array A represent consecutive cars on a road.
Array A contains only 0s and/or 1s:
- 0 represents a car traveling east,
- 1 represents a car traveling west.
- The goal is to count passing cars. We say that a pair of cars (P, Q), where 0 ≤ P < Q < N, is passing when P is traveling to the east and Q is traveling to the west.
For example, consider array A such that:
A[0] = 0 A[1] = 1 A[2] = 0 A[3] = 1 A[4] = 1
We have five pairs of passing cars: (0, 1), (0, 3), (0, 4), (2, 3), (2, 4).
Write a function:
class Solution { public int solution(int[] A); }
that, given a non-empty array A of N integers, returns the number of pairs of passing cars.
The function should return −1 if the number of pairs of passing cars exceeds 1,000,000,000.
For example, given:
A[0] = 0 A[1] = 1 A[2] = 0 A[3] = 1 A[4] = 1
the function should return 5, as explained above.
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [1..100,000];
- each element of array A is an integer that can have one of the following values: 0, 1.
비어있지 않은 A 배열은 N개의 정수로 이뤄져 있습니다.
배열 안의 각 요소들은 도로 위의 차를 표현하며, 0 또는 1로만 이뤄져 있습니다.
- 0: 동쪽으로 이동하는 차
- 1: 서쪽으로 이동하는 차
P는 동쪽으로 이동하고 Q는 서쪽으로 이동하며
0 <= P < Q < N 을 만족하는 (P, Q) 짝을 이루는 차에 대한 지나치는 차의 수를 셉니다.
만일 결과값이 1,000,000,000 을 초과할 경우에는 -1을 리턴합니다.
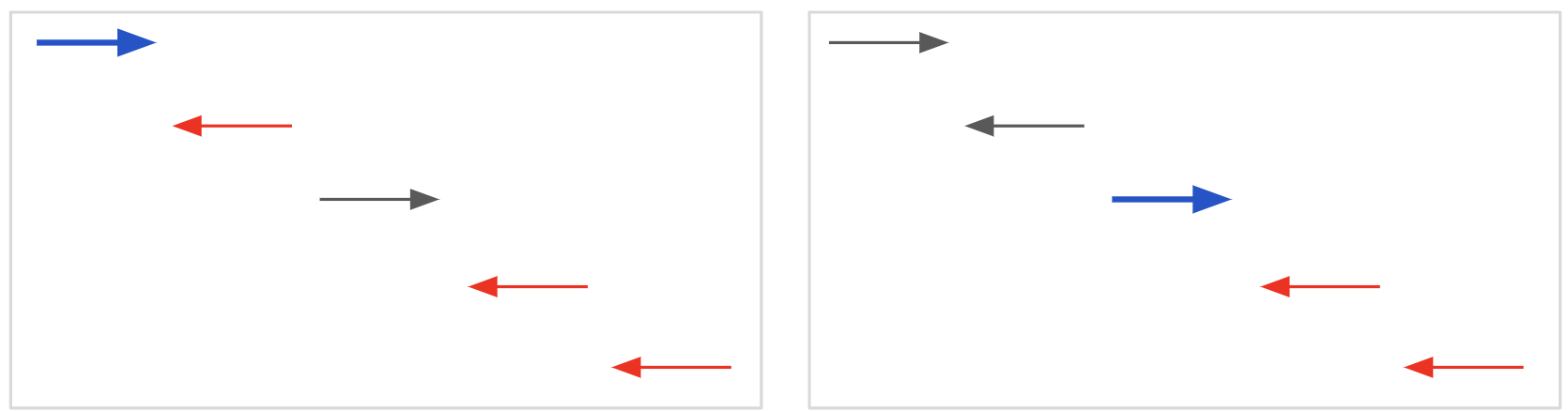
그림으로 설명하자면,
[0, 1, 0, 1, 1] 이 들어있는 배열의 경우 아래의 그림과 같고
동쪽으로 가고 있는 차를 가리키는 0이 들어있는 요소를 기준으로 해서, 그 이후 요소 중에 1이 들어있는 값들을 합산하면 됩니다.
파란색을 기준으로, 빨간색 화살표만큼을 합산하면 결과입니다.
즉, 5가 됩니다.
누적합이란?
문제의 주제가 누적합이다.
누적합을 이용하여 위의 문제를 풀어보려면 어떻게 해야할까.
codility에서 제공해주는 PDF를 참고하면, prefix sum(누적합)에 대한 정의가 쓰여있습니다.
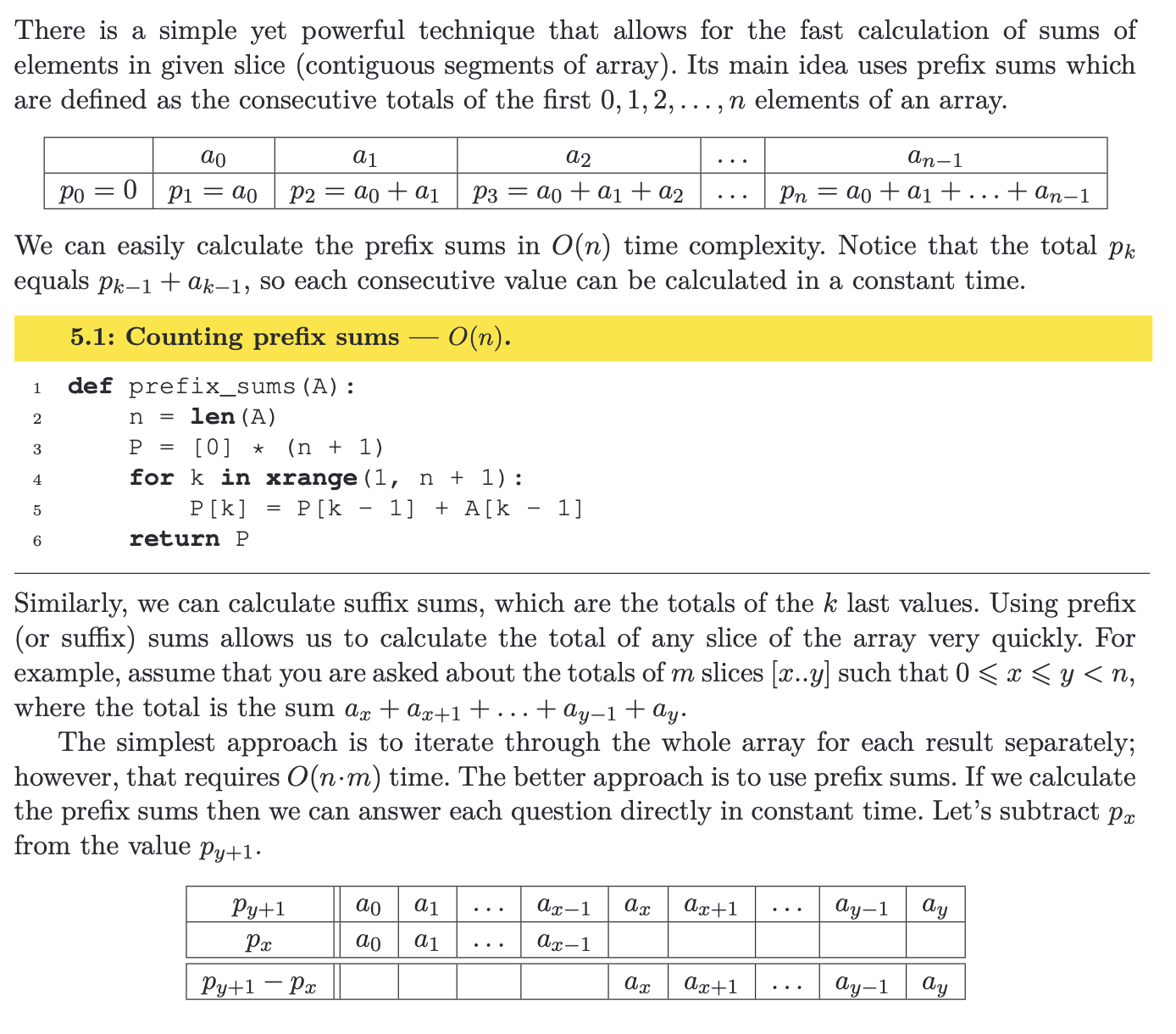
reference: Codility_ Prefix Sums
누적합을 적재할 배열 는 배열 보다 1 만큼 크기가 크고
최초의 에는 0을 넣고, 그 이후부터는 를 넣어서 누적합의 차를 빠르게 계산할 수 있게 해주는 기법입니다.
배열 A를 순회하며 누적합 배열을 만들고,
한번 더 배열을 순회하면서, 요소가 0일 경우, 현재 인덱스부터 최종 누적합의 차 만큼을 결과값에 더해주면 됩니다.
위의 화살표를 누적합 배열을 만들면
[0, 0, 1, 1, 2, 3]
이 되고,
다시 배열 A를 순회하면서 0을 만날 때 결과 result에 회수를 합산합니다.
result = (3 - 0) + (3 - 1) = 5
static int passingCars(int[] A) { int result = 0; int[] countingSum = new int[A.length + 1]; for (int i = 0; i < A.length; i++) { countingSum[i + 1] = countingSum[i] + A[i]; } for (int i = 0; i < A.length; i++) { if (A[i] == 0) { result += countingSum[countingSum.length - 1] - countingSum[i]; if(result > 1000000000) return -1; } } return result; }
'Java > coding test' 카테고리의 다른 글
| [Codility - Java] 4. Counting Elements - 3. MaxCounters (0) | 2023.01.09 |
|---|---|
| [Codility - Java] 5. Prefix Sums - 2. CountDiv (0) | 2023.01.04 |
| [Codility - Java] 7. Stacks and Queues - 1. Brackets (0) | 2023.01.02 |
| [Codility - Java] 7. Stacks and Queues - 3. Nesting (0) | 2023.01.02 |
| [Codility - Java] 7. Stacks and Queues - 2. Fish (0) | 2022.12.30 |